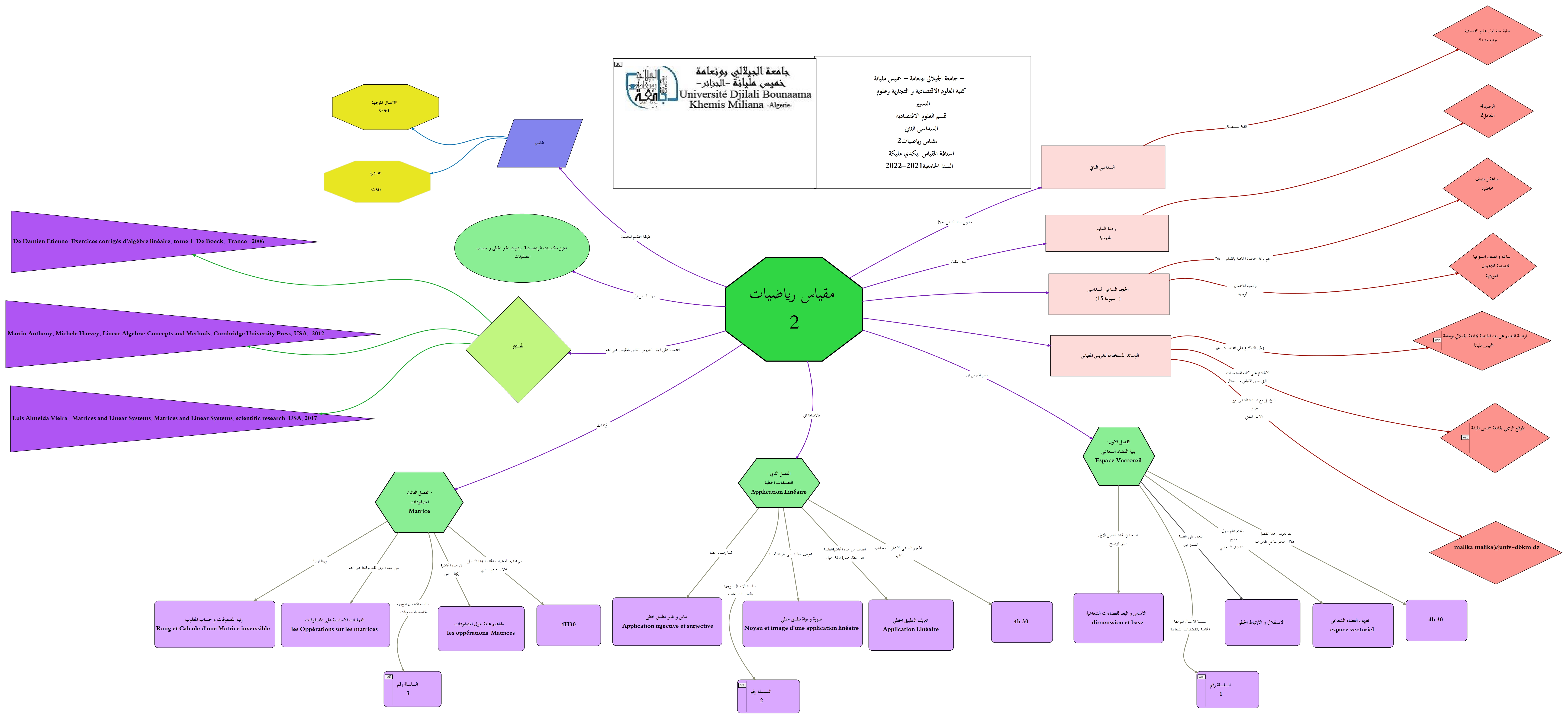
رياضيات 2
مخطط الموضوع
-
-
-
-
-
-
-
-
-
-

معلومات حول المقياس: ((Information sur le cours
الجامعة
الجيلالي بونعامة بخميس مليانـــــــــة.
الكلية
كلية العلوم الاقتصادية والتجارية وعلوم التسيير.
القسم
علوم الاقتصادية.
المستوى
السنة اولى جذع مشترك.
الميدان
علوم اقتصادية تسيير و علوم تجارية
المقياس المقرر
الرياضيات 02.
وحدة التعليم
المنهجية.
نوع الدرس
محاضرة + أعمال موجهة.
السداسي
الثاني
المعامل
02
الرصيد
4.00
الحجم الساعي
15 أسبوع في السداسي الثاني حوالي 45 ساعة
الحجم الساعي في الأسبوع
3 ساعات
المحاضرة
ساعة ونصف
الأعمال الموجهة
ساعة ونصف
نافذة التواصل
البريد الإلكتروني
يتم الرد على جميع انشغالاتكم حول المحاضرة أو الأعمال الموجهة عبر البريد الإلكتروني المهني في آجال لا تفوق 48 ساعة
الرياضيات 02 او الجبر الخطي 02 هو فرع من فروع الرياضيات يهتم بدراسة الفضاءات الشعاعية و التطبيقات الخطية و المصفوفات كما تعتبر أساساً لجميع مجالات الرياضيات تقريباً. على سبيل المثال،تعتبر الرياضيات 02 أمراً أساسياً في العروض الحديثة للهندسة، بما في ذلك تعريف الأدوات الأساسية مثل الخطوط، المستويات والدولران.
-
 الاستاذة : بكدي مليكة
الاستاذة : بكدي مليكة كلية العلوم الاقتصادية و التجارية وعلوم التسيير
قسم العلوم الاقتصادية
جامعة الجيلالي بونعامة خميس مليانة
البريد المهني : malika.bakdi@univ-dbkm.dz
ايام التواجد في المعهد: من الاحد الى الخميس من الساعة 9 الى الساعة 16
-

عند الانتهاء من هذا المقياس سيكون الطالب ملما بالأهداف التالية والتي تم صياغتها وفقا لمستويات بلوم المعرفية:
مستوى المعرفة والتذكر: أن يستعيد الطالب جل المعلومات الخاصة بمقياس رياضيات 2، إذ يتوجب عليه معرفة التعريفات و الخواص المرتبطة بموضوع الفضاءات الشعاعية. التطبيقات الخطية و المصفوفات.
مستوى الفهم والاستيعاب:أن يناقش الطالب محتوى أهمية وأهداف رياضيات 2، بالإضافة إلى تحديد الخصائص الأساسية التي تسمح بتحديد مختلف المفاهيم المتعلقة بالمحاور الرياضيات 02، وهنا نعطي الطالب بعض الأسئلة المتنوعة، انطلاقا مما تم الاستفادة منه وفهمه للدرس.
مستوى التطبيق: أن يستخدم الطالب كل المعارف ذات الصلة بموضوع الجبر الخطي او الرياضيات 02 ،كما يتعين عليه التعرف على مختلف المفاهيم المتعلقة بالفضاء الشعاعي الجزئي والأهداف المتوخاة من نظرية الاستقلال و الارتباط الخطي، التطبيقات الخطية و نوات و صورة التطبيق الخطي و كذلك المصفوفات و يجري الطالب أمثلة مختلفة عن الفضاء الشعاعي الجزئي، التطبيق الخطي انواع المصفوفات وحل جملة من التطبيقات فيما يخص الاستقلال و الارتباط الخطي انطلاقا . نواة و صورة تطبيق خطي و كذلكمختلف العمليات على المصفوفات. من الأدوات المدرجة في المحاضرة.
مستوى التحليل: يقوم الطالب بتحديد أساس فضاء شعاعي جزئي وكيف يميز بين الفضاء الذي يملك الأساس و الفضاء الذي لا يملك أساس ، وجعل الطالب يقوم بتحليل الفروقات بين المجموعة التي تشكل فضاء شعاعي جزئي و المجموعة التي لا يشكل فضاء شعاعي جزئي.ان يكون الطالب قادرا على التمييز بين صورة و نواة تطبيق خطي كيف يمكنة ان يقوم بجملة من العمليات على المصفوفات.
مستوى التركيب والإنشاء: أن يثمن الطالب وجود النظريات المتعلقة بالفضاء الشعاعي الجزئي مثل نظرية Graussmann للأبعاد ، وهنا يقوم الطالب بالعصف الذهني لإيجاد البعد فيما يتعلق بالفضاء الشعاعي الجزئي وكيفية إيجاد حلول لأبعاد أساس فضاء شعاعي جزئي انطلاقا مما استفاد منه من المحاضرة المقدمة.
مستوى التقويم:أن يكون الطالب قادرا على تحديد أساس و بعد فضاء شعاعي جزئي، بناء على المصادر والأدوات المتاحة للطالب.
-
تتطلب هذه المادة معارف مسبقة من الطالب حول التحليل الرياضي ومبادئه بالإضافة إلى إلمامه الجيد بالجانب المنهجي، كما أن الفهم الجيد لبعض الأسس النظرية السابقة لهذا المادة، يتطلب معرفة المواضيع التالية: الحساب الرياضي، الدوال بكل اشكالها، كما أنه قد يتوجب على الطالب أن يوسع اهتماماته المعرفية للكشف عن القيمة المضافة مما تعلمه حول مقياس الرياضيات 02.
-
-
-
يعد مقياس الرياضيات02 من وحدات التعليم المنهجية من عروض التكوين في نظام ل م د، يدرس في السداسي الثاني من السنة الاول ليسانس جذع مشترك ميدان علوم اقتصادية التسيير و علوم تجارية، ويحتوى هذا المقياس على الفضاءات الشعاعية، التطبيقات الخطية، المصفوفات، و المحددات، و الأنظمة الخطية باعتباره العلم الذي يدرس كيفية الايجاد الحل الأمثل للمختلف المسائل المعقدة.
تعتبر اداة ضروريا لجميع المجالات تقريباً. على سبيل المثال، تعتبر الفضاءات الشعاعية خطوة مهة جدا في العروض الحديثة لـ الهندسة، بما في ذلك تعريف المتغيرات الأساسية مثل الخطوط، المستويات و الابعاد.
تستدم كذلك في مجال الاقتصاد و دراسة الأنظمة المعقدة و تحليل البايانات. ففي مجال الاقتصاد مثلاتعتبر الرياضيات 02 الطريقة الامثل في حل النماذج المعقدة بأكثر كفاءة و دقة من خلال تقريب العديد من العلاقات الاقتصادية وتحويلها إلى معادلات خطية، ومن الأمثلة الاكثر تداولا على تطبيقات الرياضيات 02 في الاقتصاد هو نموذج (LeontiffInput-output) حيث يقوم على تقسيم الاقتصاد إلى قطاعات مختلفة مثل صناعة الفحم، والصناعة الزراعية، والصناعة التحويلية واستخدام المعادلات الخطية المناسبة لكل قطاع .فالفهم الجيد للمفاهيم الاساسية التي تبنى عليها الرياضات 02 هام لفهم و تبسيط العديد من المشاكل المتعلقة بمختلف المجالات. بالنسبة إلى أنظمة النظام غير الخطي، لا يمكن نمذجتها باستخدام خواص الرياضيات 02.
يهدف مقرر الرياضيات 02 لتقديم المفاهيم الأساسية في علم الجبر اعتماداً على حاجات الطالب المتوقعة في دراسته في هندسة نظم المعلومات وتحليل المعطيات و غيرها من المجالات. فهو يحتاج إلى مفهوم الفضاء الشعاعي لدراسة بنية مجموعة ما بالنسبة لعلاقات وعمليات يتم تعريفها على عناصر هذه المجموعة، ورؤية الهيكل التنظيمي لهذه المجموعة وفق الروابط بين عناصرها. ثم العلاقات بين الفضاءات الشعاعية والتي يُعبرّ عنها بوساطة التطبيقات الخطية. وبعد ذلك ندرس المصفوفات وعلاقتها بالتطبيقات الخطية، ثم المحددات وحل جمل المعادلات الخطية.
يحتوي المقياس على أربعة محاور أساسية حيث أن كل محور يأتي ضمن تسلسل بيداغوجي يسمح بفهم واستيعاب المفاهيم الأساسية التي تم التطرق إليها من خلال المحاضرة، أما من خلال حصة الأعمال الموجهة فيتم تدعيم دروس التعلم بسلسة من التمارين والتي تساعد الطلبة على الفهم والاستيعاب أكثر للمفاهيم بالإضافة إلى إسقاط الجانب النظري على الجانب التطبيقي واستخلاص ما يمكن استخلاصه، وتتمثل هذه المحاور التي تشكل المحاضرة في:
· مقدمة.
· المحور الأول: بنية الفضاء الشعاعية.
· المحور الثاني: التطبيقات الخطية.
· المحور الثالث: المصفوفات.
· المحور الرابع :الأنظمة الخطية
· خاتمة.
-
-
الفضاء المتجهي أو الفضاء الشعاعي يعتبر عنصر أساسي في دراسة الجبر الخطي. هو مجموعة من عدة متجهات والتي يمكن إضافتها مع بعضها البعض وضربها بأعداد، التي يطلق عليها بالسلاميات. غالبا ما تكون السلميات عبارة عن أعدادا حقيقية، ولكن بالإمكان اختيار فضاءات شعاعية مع السلميات من أعداد مركبة . عمليتا جمع الأشعة وضرب شعاع ما في سلمية ينبغي لهما أن تحققا مجموعة من المتطلبات تدعى بالقانون الداخلي و القانون الخارجي. سنتطرق إلى كل هاتي المفاهيم بتفصيل في هذا الفصل .
-

-
ماهي خصائص فضاء شعاعي جزئي
-
-
-
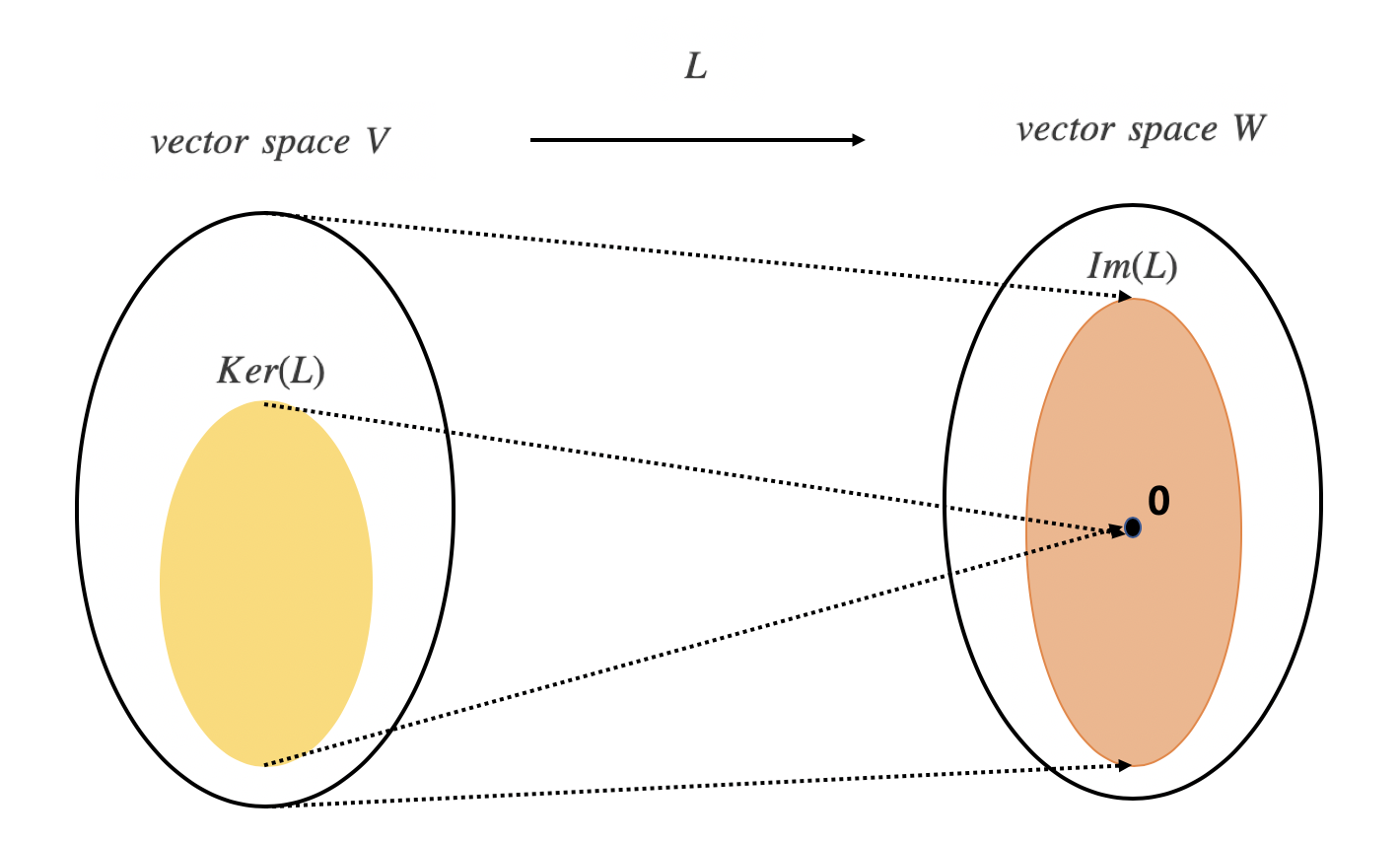
تناول هذا المحور جانب مهم في الجبر الخطي ألا وهو التطبيقات الخطية حيث ترد التطبيقات الخطية في معظم العلوم الرياضية البحتة (ولاسيما الجبر، والهندسة، والتحليل الرياضي، وغيرها). وفضلاً على ذلك فإنها تستعمل في فروع تطبيقية لها فوائد عملية كثيرة. أهم هذه الفروع:
البرمجة الخطية "la programmation linéaire " ، التي تدرس الوصول إلى الحد الأعلى أو الأدنى لتطبيق خطي خاضع لقيود معطاة. وللبرمجة الخطية استعمالات مفيدة جداً في العلوم الاقتصادية وتخطيط الإنتاج.
نظرية الألعاب " la théorie des jeux "، التي لها فوائد جلى في تحديد الاستراتيجيات.
عند الانتهاء من هذا المحور سيكون الطالب ملما بالأهداف التالية والتي تم صياغتها وفقا لمستويات بلوم المعرفية:
مستوى المعرفة والتذكر:أن يستعيد الطالب أهم المفاهيم الخاصة بالدوال و الأبعاد، وكذلك معرفة اهم المجموعات التي تشكل فضاءات شعاعية ، حتى يتسنى له معرفة مجموعة البدء و الوصول الخاصة بكل تطبيق.
مستوى الفهم والاستيعاب:أن يناقش الطالب محتوى أهمية وأهداف التطبيقات الخطية والمتمثلة في كل من: (النواة ، و الصورة ، تطبيق خطي متباين و غامر) ، بالإضافة إلى تحديد الخصائص الأساسية لكل من النواة و الصورة.
مستوى التطبيق: أن يكون الطالب قادرا على إسقاط وتوظيف مدلول كل عنصر من عناصر التطبيق الخطي ..
مستوى التحليل: أن يكون الطالب قادرا على تحديد ما إذا كان التطبيق الخطي غامر أو متباين، من خلال تشخيصه الدقيق لكل عنصر من عناصر التطبيق الخطي، وهو ما يسمح له تحليل وبحث عن نواة و صورة تطبيق خطي.
مستوى التركيب والإنشاء: أن يثمن الطالب مفهوم التطبيق الخطي وعلاقته بالفضاء الشعاعي الجزئي.
مستوى التقويم:أن يكون الطالب قادرا على تحديد عناصر التطبيق الخطي (النواة، بعد النواة، الصورة، بعد صورة تطبيق خطي) ، بالإضافة إلى دراسة ما إذا كان التطبيق عبار عن تطبيق تشاكلي.
-
-
هل نواة التطبيق الخطي عبارة عن فضاء شعاعي جزئي
-
-
Opened: السبت, 11 يونيو 2022, 12:00 AMDue: السبت, 18 يونيو 2022, 12:00 AM
-
-
-
-
المراجع باللغة العربية :
1. . بركات الخير. مخلوف ساسية. بوضياف نعيمة . شطوح كريمة. حدوش وردة. الوافي هشام- 1 كلية العلوم الإقتصادية والتجارية وعلوم التسيير قسم التعليم الأساسي جامعة العقيد الحاج لخضر - باتنة
دروس وتطبيقات II مادة الرياضيات السداسي الثاني لطلبة السنة الأولى .
2. د. معروف عبدالرحمان سمحان, د. علي عبدالله السحيباني, د. فوزي أحمد الذكير. الجبر الخطي وتطبيقاته. جامعة الملك سعود. ا لعبيكان للنشر . السعودية.
3. مجدي طويل . المصفوفات النضرية و التطبيق . كلية الهندسة جامعة القاهرة .1996.
4. میسم أحمد جدید. منشورات جامعة الشام الخاصة كلية الهندسة المعلوماتية رياضيات 1. 2020.
المراجع باللعة الفرنسية :
1. De Damien Etienne, Exercices corrigés d’algèbre linéaire, tome 1, De Boeck, France, 2006.
2. Daniel Guinin, Bernard Joppin, Algèbre et géométrie PC, Editions Bréal, France, 2004.
3. Camille Debiève, Yves Félix, Algèbre linéaire: Pour HEC et ingénieurs commerciaux, De Boeck, France, 2000.
4. Djamel Berkane, exercice d’entrainement , algèbre,
5. Mohamed Hazi, Analyse et Algèbre de première annéé des universités et grande écoles scientifiques, tome 1, 3iem édition, office des publications universitaires, 2004.
6. Mohamed Hazi, Analyse et Algèbre de première annéé des universités et grande écoles scientifiques, tome 2, 3iem édition, office des publications universitaires, 2004.
المراجع باللغة الانجليزية :
- Harold M. Edwards, Linear Algebra, Springer Shop, USA, 1995.
- Martin Anthony, Michele Harvey, Linear Algebra: Concepts and Methods, Cambridge University Press, USA, 2012.
- Serge Lang, Linear Algebra, Springer Shop, third edition, USA, 2004.
- Steeve Sarfati, Matthias Fegyvères, Mathématiques: méthodes, savoir-faire et astuces, Editions Bréal, France, 1997.
- Renzo Cairoli, Algèbre linéaire, PPUR presses polytechniques, France, 1991.
- Robert C. Dalang, Amel Chaabouni, Algèbre linéaire: aide-mémoire, exercices et applications, PPUR presses polytechniques, France, 2004.
-

-
-
-
-