مخطط الموضوع

  • عام

    طي الكل توسيع الكل
    • forum icon
      رياضيات2 المنتدى 
         يتمحور مقياس رياضيات2 الموجه لطلبة السنة أولى ليسانس علوم اقتصادية وتجارية وعلوم التسيير حول المفاهيم المتعلقة بجانب الجبر
الخطي، ويعتبر كتكملة لجانب التحليل الذي تم التطرق إليه في مقياس رياضيات1 ، 
      حيث يهتم  المقياس بكل ما يخص الفضاءات الشعاعية، التطبيقات الخطية، المصفوفات، والأنظمة الخطية 


      .
    • forum icon
      منتدى الطلبة المنتدى


  • التعريف بالمقياس



    المستوى: السنة أولى علوم اقتصادية وتجارية وعلوم التسيير -جذع مشترك-

    وحدة التعليم: منهجية

    مقياس: رياضيات2               الرصيد: 04                   المعامل: 02

    يتمحور مقياس رياضيات 2 حول المفاهيم المتعلقة بجانب الجبر الخطي، حيث يهتم هذا الجانب 

    بكل ما يخص الفضاءات الشعاعية، التطبيقات الخطية، المصفوفات، والأنظمة الخطية.


  • معلومات الاتصال


    أستاذة المقياس: بوكريطة خديجة

    كلية العلوم الاقتصادية والتجارية وعلوم التسيير 

    قسم العلوم التجارية

    جامعة الجيلالي بونعامة خميس مليانة

    البريد الالكتروني: k.bokreta@univ-dbkm.dz
    أيام التواجد في الكلية: الاثنين من 10:30 إلى 15:30 والثلاثاء من 10:30 إلى 13:30



  • مساحة التواصل

  • أهداف المقياس



    عند الانتهاء من هذا المقياس سيكون الطالب ملما بالأهداف التالية:

    1/ يتعرف الطلاب على مختلف المفاهيم المتعلقة بمحاور الرياضيات 2 مع تحديد الخصائص الأساسية لكل محور.

    2/ يقوم الطلاب بالتمييز بين أجزاء كل محور، من خلال التفريق بين كل من مفاهيم التركيبات الخطية، الارتباط والاستقلال الخطي،

     صورة ونواة تطبيق خطي، وتطبيق مختلف العمليات على المصفوفات.

    3/ يربط الطلاب بين مختلف المفاهيم الأساسية المقدمة الخاصة بالفضاء الشعاعي الجزئي وتركيبها مع كل من مفهوم الأساس والبعد،

     التطبيق الخطي، وجمل المعادلات الخطية، مما يساعدهم على إيجاد الحلول للمسائل المقدمة.

    4/ يتم تقييم الطلاب عن طريق تمارين شاملة تتضمن كل ما تم التطرق إليه فيما يخص الفضاءات الشعاعية، التطبيقات الخطية، المصفوفات، وجمل المعادلات الخطية.

  • المكتسبات القبلية



    يتوجب على الطالب المقبل على دراسة مقياس رياضيات2  أن يكون ملما بجانب التحليل الذي تم التطرق إليه في مقياس رياضيات1 

    والذي تم فيه اكتساب مهارة التحليل الرياضي التطبيقي، طرق الحساب الرياضي، ومعالجة الدوال بأشكالها.

  • خطة العمل



  • المقدمة العامة



    يعد الجبر الخطي أداة رياضية ضرورية لدراسة مواضيع مختلفة مثل الفيزياء والكيمياء والاقتصاد والإحصاء وعلم الاجتماع، وقد أصبح في السنوات الأخيرة يشكل جزءا أساسيا من الخلفية الرياضية المطلوبة في كثير من العلوم.

    وقد نشأ الجبر الخطي من دراسة جمل المعادلات الخطية التي بدأها Leibnitz في عام 1678، ثم تابعها Maclaurin عام 1748، وأكملها Cramer في عام 1754؛ ومن جهة أخرى ظهر مفهوم المصفوفة عند Gauss، كما عرف  Cauchyكثير الحدود المميز للمصفوفة في عام 1826.

    ومن ثم تطورت نظرية المصفوفات في منتصف القرن التاسع عشر على يد كل من Cayley و Sylvester، وأصبحت المفاهيم الجديدة متعارفة ومألوفة أكثر فأكثر، مما أفسح المجال لظهور مفهوم الفضاء الشعاعي من طرف كل من Cayley و Grassman، وأخيرا صاغ Peano عام 1888  التعاريف المبنية على موضوعات أولية للجبر الخطي.

    وبذلك يحتوي برنامج مقياس الرياضيات2 على المعارف الأساسية في الجبر الخطي اللازمة لدراسات الطالب اللاحقة، من هندسة نظم المعلومات وتحليل المعطيات وغيرها من المجالات، أي بكل ما يتعلق بالفضاءات الشعاعية والعلاقات بينها المعرفة بواسطة التطبيقات الخطية، وكذلك طرق حساب المصفوفات وحل جمل المعادلات الخطية.

  • المحور الأول: الفضاءات الشعاعية



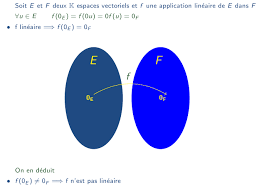
    من خلال المحور الخاص بالفضاءات الشعاعية:

    1/ يتعرف الطلاب على الخصائص الأساسية للفضاءات الشعاعية مع تحديد مختلف المفاهيم المتعلقة ببنية الفضاء الشعاعي الجزئي.

    2/ يقوم الطلاب بالتمييز بين العناصر الرئيسية للدرس وأجزائه، من خلال التفريق بين كل من مفاهيم التركيبات الخطية، الارتباط الخطي والاستقلال الخطي.

    3/ يربط الطلاب بين مختلف المفاهيم الأساسية المقدمة وتركيبها مع مفهوم الأساس والبعد مما يساعدهم على إيجاد الحلول للمسائل المقدمة.

    4/ يتم تقييم الطلاب عن طريق تمارين شاملة تتضمن كل ما تم التطرق إليه فيما يخص الفضاءات الشعاعية.

  • المحور الثاني: التطبيقات الخطية



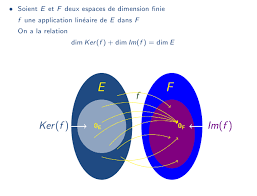
    من خلال المحور الخاص بالتطبيقات الخطية:

    1/ يتعرف الطلاب على المفاهيم الأساسية المتعلقة بفضاء التطبيقات الخطية والعلاقة بينها.

    2/ يقوم الطلاب بالتمييز بين العناصر الرئيسية للدرس وأجزائه، من خلال التفريق بين مفهوم  صورة تطبيق خطي ونواة تطبيق خطي.

    3/ يربط الطلاب بين مختلف المفاهيم المقدمة وتركيبها مع مفهوم بعد فضاء شعاعي ورتبة تطبيق خطي  للتمكن من حل المسائل المقدمة.

    4/ يتم تقييم الطلاب عن طريق تمارين شاملة تتضمن كل ما تم التطرق إليه فيما يخص التطبيقات الخطية.

  • وظيفة


  • الاختبار النهائي (الخروج)


  • المراجع



    بابا حامد، محاضرات في التحليل، ديوان المطبوعات الجامعية، 1988

    سعود محمود، التحليل الرياضي، ديوان المطبوعات الجامعية، 2009

    حسن رجب محمد، أساسيات الرياضيات الجبر والهندسة التحليلية والإحصاء ، دار الفجر للنشر والتوزيع مصر 2000،

    - L. Amyotte, Introduction à l'algèbre linéaire et à ses applications, 2ème éd., kanada: édition du renouveau pédagogique INC, 2003.

    - J. Cellier, Algèbre linéaire: des bases aux applications, Rennes: presses universitaires de Rennes, 2008.

    - Y. Dodge, Mathématiques de base pour économistes, Paris, Springer, 2002.

    - B. Guerrien, Algèbre linéaire pour économistes, 4ème éd., Paris, Economica, 1997.

    - P. Tauvel, Exercices d'algèbre générale et arithmétique: 470 énoncés avec solutions détaillées, Paris, Dunod, 2004.

    - G. Patrik, Mathématiques pour l'économie: méthodes et exercices corrigés, Belgique : de boeck, 2005.

    - J. Vauthier et all., Exercices de Mathématiques, L1 et L2, 1re et 2e année d’Université, Algèbre, Analyse, Géométrie. Edition ESKA, Paris, 2006

  • مساحة الممتحنين (Testeurs)