Cours : رياضيات 2

Généralités

Annonces Forum

التعريف بالمقياس

المستوى : السنة الأولى جذع مشترك (السداسي الثاني)

1- معلومات حول المقياس: ((Information sur le cours
الجامعة	الجيلالي بونعامة بخميس مليانـــــــــة.
الكلية	كلية العلوم الاقتصادية والتجارية وعلوم التسيير.
القسم	جذع مشترك سنة أولى
المستوى	السنة الأولى
التخصص	جذع مشترك
المقياس المقرر	رايضايات 02
وحدة التعليم	المنهجية.
نوع الدرس	محاضرة + أعمال موجهة.
السداسي	الثاني
المعامل	02.
الرصيد	04.
الحجم الساعي	14 أسبوع في السداسي الثاني حوالي 42 ساعة	الحجم الساعي في الأسبوع	3 ساعات
		المحاضرة	ساعة ونصف
		الأعمال الموجهة	ساعة ونصف
نافذة التواصل	البريد الإلكتروني	nadjet.benfreiha@univ-dbkm.dz	يتم الرد على جميع انشغالاتكم حول المحاضرة أو الأعمال الموجهة عبر البريد الإلكتروني المهني في آجال لا تفوق 48 ساعة

يشمل مقياس الرياضيات 02 المواضيع المقررة في برنامج السداسي الثاني لطلبة السنة الأولى ل . م . د علوم اقتصادية وتجارية وعلوم التسيير.

وتعتبر المواضيع المقدمة فيه كترسيخ وتتمة لما درس في القسم النهائي في الطور الثانوي، والتي من المفروض ان يكون الطالب ملما بها الماما جيدا ماعدا بعض الفصول الجديدة التي لم يسبق له دراستها.

وتم تصميم الدروس وفقا لاحتياجات طالب العلوم الاقتصادية والتجارية وعلوم التسيير لما يتفق مع ما يستخدمه من الرياضيات في بقية مقاييس دراسته بعيدا عن الالتواءات والتعقيد الذي يولد الصعوبات بحدود الممكن ومراعاة المقرر.

حيث تم الاستعانة بأمثلة وتمارين توضيحية وكذا سلاسل تمارين بسيطة يتحوي على أكثر من مثال للحل وهذا لمساعدة الطالب على ترسيخ المعلومات المقدمة له.

معلومات الاتصال

الاستاذة: بن فريحة نجاة

قسم العلوم الاقتصادية، كلية العلوم الاقتصادية والتجارية وعلوم التسيير ، جامعة الجيلالي بو نعامة ، خميس مليانة

البريد الالكتروني: nadjet.benfreiha@univ-dbkm.dz

يتم الرد على جميع انشغالاتكم حول المحاضرة أو الأعمال الموجهة عبر البريد الإلكتروني المهني في آجال لا تفوق 48 ساعة

مساحة التواصل

أهداف المقياس

في نهاية هذا المقياس يجب أن يكون الطالب قادر على حل المعادلات والدوال والمصفوفات، فالأهداف المرجوة من هذا المقياس تتمثل فيما يلي:

- تمكين الطالب من استيعاب مفهوم المعادلة التفاضلية و المشتقات الجزئية لاستعمالها في الاقتصاد الجزئي.

- التعامل مع المصفوفات من أجل توظيفها في مجالات ذات صلة مع تخصص العلوم الاقتصادية كرياضيات المؤسسة وبحوث العمليات وتحليل المعطيات ...الخ.

- توظيف المفاهيم الأساسية حول المصفوفات في حل جمل معادلات خطية كي تستعمل لاحقا في نظرية اتخاذ القرار.

المكتسبات القبلية

تتطلب هذه المادة معارف مسبقة من الطالب حول مفهوم الرياضيات بالإضافة إلى إلمامه الجيد بالجانب الرياضي من حيث التطبيقات الرياضية والقوانين الاساسية، لكي يستطيع الطالب استيعاب هذا المقياس، يجب أن يكون على دراية بـ: الرياضيات1، وهذا ليسهل على الطالب حل المعادلات الرياضية التفاضلية والدال وكذا المصفوفات، كما أنه قد يتوجب على الطالب أن يوسع اهتماماته المعرفية للكشف عن القيمة المضافة مما تعلمه حول مقياس الرياضيات 02.

ينبغي أن يكتسب ويمتلك كل من يدرس الرياضيات، العديد من الخبرات والمهارات والقدرات، التي تسمح لك بالتحكم الجيد في المقياس، ومن هذه المكتسبات:

- الرغبة في التطوير الذاتي والاجتهاد في التخصص.

- مهارات رياضية وحسابية.

- الالمام بمختلف المفاهيم الاولية في الجبر والتحليل.

سؤال مكتسبات قبلية Test

مخطط المقياس

أعزائي الطلبة نضع بين ايديكم مخطط لمقياس الرياضيات 02 والذي يحتوي على تفصيل لجميع المحاور المبرمجة عليكم

plan de cours Fichier

Déposé le 18 févr. 23, 14:31

المقدمة العامة

This animation shows a stick figure behind a podium using a pointer to present.

مقياس الرياضيات 02 موجه لطلبة السنة الأولى جذع مشترك، وقد تم تقسيمه إلى خمسة محاور، أما المحور الأول فقد ركزنا فيه على المعادلات التفاضلية من خلال التعريف بها وتحديد أنواعها والتطرق الى أهم طرق الحل االمعتمدة بالنسبة للمعادات من الدرجة الاولى والمعادلات من الدرجة الثانية. وخصصنا لهذا المحور محاضريتين.

أم المحور الثاني فقد تضمن الدوال ذات متغيرين متطرقين بذلك الى التعريف بالدالة ذات متغيريين والتطرق الى الاشتقاق الجزئي من الرتبة الاولى والاشتقاق الجزئي من الرتبة الثانية، مخصصين لهذا المحور مدة أسبوعين.

بالنسبة للمحور الثالث فقد تضمن المصفوفات والعمليات عليها حيث تطرقنا به الى التعريف بالمصفوفة وأنواعها وكذا العمليات الاساسية عليها. وفي حدود محاضرتين.

أما المحور الرابع محدد ومقلوب مصفوفة فقد تطرقنا فيه الى محددات المصفوفة من الرتبة الثانية، محدد المصفوفة من الدرجة الثالثة (قاعدة سارس، طريقة المحددات الصغرى)و خواص المحددات وكذا التعريف بمقلوب المصفوفة وايجادها، والتطرق الى خصائصها مخصصين لذلك 3 محاضرات.

وأخيرا المحور الخامس حل جملة المعادلات الخطية والذي تطرقنا به الى: كتابة جملة المعادلات على الشكل المصفوفي، حل جملة معادلات خطية بطريقة كرامر Cramer، حل جملة معادلات خطية بطريقة مقلوب المصفوفة، حل جملة معادلات خطية بطريقة غوس Gauss، حل جملة معادلات خطية باستخدام المحددات، وأخيرا حل جمل معادلات خطية في حال مصفوفتها المرفقة غير قابلة للقلب مخصصين لذلك 5 أسابيع.

ملاحظة : حيث خصصت لكل محور سلسلة من التمارين موجهة الى الطلبة حتى يتمكن الطالب من الاستيعاب أكثر وترسيخ المعلومات التي يتلقاها في المحاضرة.

مقدمة المحور الاول: المعادلات التفاضلية

ظهرت المعادلات التفاضلية أولاً مع اختراع حساب التفاضل والتكامل من قبل نيوتن ولايبنز . في العام 1761 ، قام إسحاق نيوتن في الفصل الثاني من كتابه طريقة التدفقات، بإدراج ثلاثة أنواع من المعادلات التفاضلية:

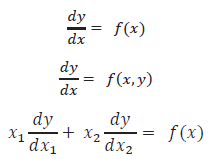
وفي عام 1695 اقترح جاكوب بيرنولي معادلة بيرنولي التفاضلية.والتي حاول لايبنز حلها من خلال تبسيطها في العام التالي .

وتعود الدراسات الاولى لما يسمى حاليا بالمعادلات التفاضلية من الرتبة الاولى المتجانسة الى العام 1734 لـ Alexis Clairaut بعدها طور كل من Lagrange et Euler الطريقة التي استخدمها Clairaut .

وفي العام 1739 في مسالة تدرس الاهتزازات ظهرت لـ Euler معادلة تفاضلية من الرتبة الرابعة ذات معاملات حقيقية، وتمكن هذا الاخير من وضع ما نسميه الان بالمعادلة المميزة للمعادلة التفاضلية في العام 1743 . كما قدم Lagrangeاساسيات حل معادلة تفاضلية غير متجانسة.

تاريخيًا، درست مسالة اهتزاز حبل ما، حبل آلة موسيقية مثالاً، من طرف كل من لوران دالمبير وليونارد أويلر ودانييل برنولي وجوزيف لوي لاغرانج . وفي عام 1677، اكتشف لوران دالمبير معادلة الموجة أحادية البُعد وبعد عشر سنين، اكتشف أويلر معادلة الموجة ثلاثية الأبعاد.

المحور الاول: المعادلات التفاضلية

تذكير:

اليك بعض المشتقات للتذكير :

المعادلات التفاضلية:

لتكن y دالة للمتغير x قابلة للاشتقاق n مرة نسمي معادلة تفاضلية من الرتبة n كل

معادلة من الشكل:

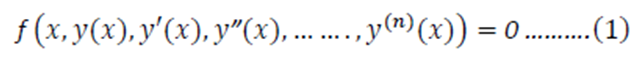
حيث: y⁽ⁿ⁾ هي المشتقة النونية لـ y

يسمى الشكل العام لـ y(x) الذي يحقق المعادلة (1) بالحل العام للمعادلة التفاضلية . ونسمي حل خاص للمعادلة التفاضلية كل حل يحقق بعض الشروط الخاصة و تسمى هذه الشروط بالشروط الابتدائية .