Matérialisation d'un grafcet
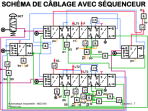
Matérialisation d'un Grafcet par un séquenceur câblé
Un Grafcet est constitué d'un certain nombre d'étapes. A chaque étape i, on associe une variable booléenne Xi représentant son activité (Xi=1: l'étape i est active, Xi=0: l'étape i est inactive). Il est alors possible de matérialiser Xi par la variable de sortie Qi d'une bascule (RS, JK ou D). La synthèse de l'automate consiste à calculer les entrées (Ri, Si, Ji, Ki ou Di) de ces bascules en fonction des variables Xi et des réceptivités associées aux transitions du Grafcet.
Il reste à résoudre le problème du marquage initial: les bascules correspondantes aux étapes initiales doivent être mises à 1 et les autres à 0. On utilise pour cela une entrée d'initialisation I qui permet de forcer les bascules dans la configuration initiale.
Exemple :
 |
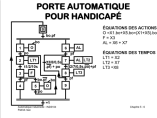
matérialisation d'un grafcet avec automate programmable
Remarque :
la partie automate programmable sera présenter dans le chapitre qui suit.
Types d'Entrées/Sorties (E/S):
1. TOR (tout ou rien) : 0-5 volts (TTL), 0-24 volts, 0-48 volts, 0- 220 volts
2. Analogiques : pour mesurer des pressions, températures..
0-10 Volts (boucle de tension) 4-20 milliampères (boucle de courant)
3. numériques : valeur binaire sur N bits: code à barre
materialisation du grafcet
Pour matérialiser un Grafcet sur un automate nous allons
procéder par gestion autours des transitions. Le programme contient
successivement :
• La programmation des échanges (mnémonique ECH) : cette
gestion est effectuée par l'automate.
• L'animation du Grafcet qui est décomposée en trois
sous-ensembles :
Le calcul des infroissabilité (mnémonique FRA)
la
franchissabilité d'une transition est une variable logique notée Fi qui vaut 1 si et seulement si cette transition peut être franchie.
Autrement dit il faut que les étapes immédiatement précédantes soient actives et que la réceptivité associée à cette transition soit vraie. Ainsi Fi=Xi-1.Ci .
Le franchissement des transitions (mnémonique FTR)
pour chacune des transitions on évalue sa infroissabilité (Fi) et lorsqu'elle est vraies on désactive les étapes immédiatement précédentes et on active les étapes immédiatement suivantes si Fi=0 l'état du Grafcet reste inchangé. Ainsi Xi≅Fi et Xi+1≅Fi.
Le calcul des variables de retard (mnémonique RET)
dans le cas où le Grafcet contient des réceptivités dynamiques on utilise des variables de retard notées M* afin de modéliser les fronts d'une
variable. Ainsi on a: ↑M=M.M* . Cette valeur M* est en fait la valeur de M au cycle d'automate précédant :
![]()
• L'initialisation (mnémonique INI) : Le but de cette partie est d'activer les étapes initiales et de désactiver toutes les autres. On utilise pour cela une variable booléenne supplémentaire
notée I de la façon suivante :
Étape initiale : Xi≅I
Étape non initiale : Xi≅I
• Les actions (mnémonique ACT) : Les actions sont calculées dans cette dernière partie en fonction de l'activité des étapes et des conditions qui leur sont associées :
Action simple : A=Xi action inconditionnelle
A=Xi.c action conditionnelle
Action mémorisée :
A≅Xi action inconditionnelle mémorisée à l'appel
A≅Xi.c action conditionnelle mémorisée à l'appel
A≅Xi action inconditionnelle mémorisée à la retombée
A≅Xi.c action conditionnelle mémorisée à la retombée
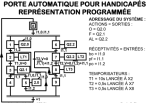
• Structure d'un programme littéral :
ECH : Gestion des échanges.
FRA : Calcul des franchissabilités.
FTR : Calcul des franchissements.
RET : Calcul des variables de retard.
INI : Initialisation du Grafcet.
ACT : Calcul des actions.
exemple d'application
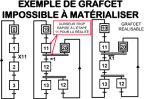 | Exemple d'un grafcet à matérialiser |
 |
 |
 | Avec automate programmable |
 |
 |






